佐賀大学農学部応用生物科学科　情報基礎演習　講義テキスト　　科目ホームページ

相関と回帰

2つの連続変量の間の関係を見る方法として、相関係数と回帰係数があります。

相関係数(単相関、Pearsonの積率相関)

相関係数とは2つの連続変量の間の関係を示す統計量で、散布図を描くと 2つの連続変量が右上がりの傾向を示す時には正の相関、右下がりの傾向を示す時には負の相関があります。相関係数の値は-1から+1までで、絶対値が大きくなるほど強い相関があり、散布図を描くと直線に近い形になります。一方、絶対値が小さくなるほど相関は弱くなり、散布図を描くと全体にばらついてしまいます。

注意事項

相関係数を算出する前に必ず散布図を描いてください。全く異なる反応をしている複数の集団をまとめて相関係数を計算してしまいますと、低い相関しか得られません。
強い因果関係がある場合には、必ず強い相関が得られますが、逆は必ずしも真ではありません。因果関係を立証するためには、そのための注意深い実験計画を立てる必要があります。
検定時の帰無仮説は「無相関」です。従って、有意な相関係数とは言っても「このデータからは無相関とは断定できない」という程度のものでしかありません。通常、絶対値が0.4以上で中程度の相関、絶対値で 0.6以上で高い相関と考えてください。
2つの変量の順位について相関を見る、順位相関係数というものもあります。データが正規分布から大きくはずれる場合には有効です。

直線回帰(単回帰)

直線回帰とは2つの連続変量を説明変量(独立変量)と目的変量(従属変量)に区別して、説明変量の値から目的変量の値を推定するための回帰式を求める手法です。

直線回帰モデル: y = a + xb + e

ここで、yは目的変数ベクトル、xは説明変数ベクトル、 eは誤差ベクトル、aとbはパラメータで、aは定数項、bは回帰係数です。

検定には回帰係数に関するt検定と、モデルに関するF検定(分散分析)があります。回帰係数の標準誤差や信頼区間も算出できます。

注意事項

相関係数が低い値の場合には、直線回帰を使用することはできるだけ避けてください。
できるだけ残差プロットをしてください。残差プロットに一定の傾向や周期性が認められる場合には、モデルに変数を追加したり、データを事前に補正する必要があります。

例題

Excelの分析ツールを使って、相関係数を算出し、回帰分析を行います。

ウズラSS系統77世代の雄の体重データについて0週齢体重と6週齢体重の相関係数を計算し、直線回帰式を求めます。まず、ここを右クリックして「リンクを名前を付けて保存」を選択してデータをダウンロードします。

Excelを起動して、gwdata.csvを読み込みます。左から個体ID、0週齢体重、1週齢体重、......10週齢体重、12週齢体重、15週齢体重が入力されています。

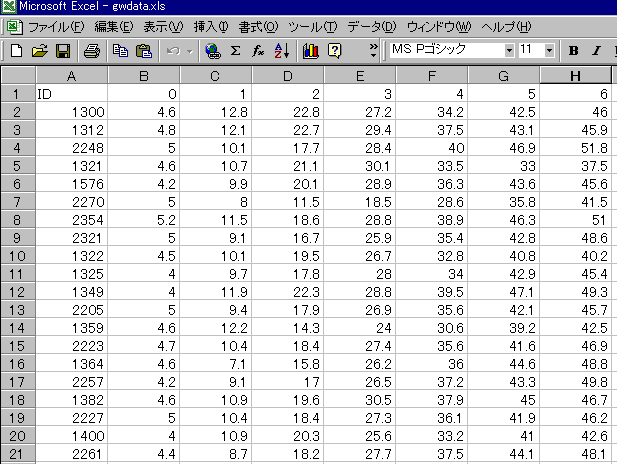
0週齢体重の列を「編集」「コピー」して、sheet2の左端に「貼り付け」ます。同様に6週齢体重の列もsheet2の0週齢体重の右側に貼り付けてください。

「ツール」の「分析ツール」の「相関」を選択します。「分析ツール」が見当たらない場合には、「アドイン」の「分析ツール」のところにチェックを入れてOK ボタンを押してください。

入力範囲を指定して、「先頭をラベルとして使用」にチェックを入れてOK ボタンを押します。相関係数が0.34と算出されました。

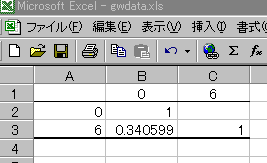
続いて0週齢体重から6週齢体重を予測する直線回帰式を求めます。「分析ツール」の「回帰分析」を選択して、Yの範囲を6週齢体重に、 Xの範囲を0週齢体重に指定します。「ラベル」にチェックを入れます。「残差グラフの作成」と「観測値グラフの作成」にもチェックを入れておきましょう。

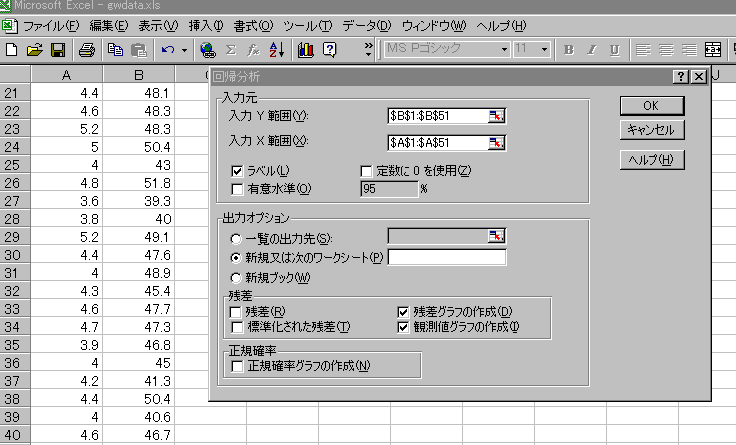
切片34.20、回帰係数2.66の直線回帰式を求めることができました。分散分析の結果は5%水準で有意で、残差のグラフを見ても、観測値のグラフを見ても系統誤差は確認されませんでした。従って、0週齢体重と6週齢体重には直線的な関係があることがわかります。ただし、寄与率R2が0.116ですので、0週齢体重から6週齢体重を予測するには精度が低いということになります。

大学院生、編入学生、転学生、募集中！

最終更新年月日 2010年1月5日

佐賀大学農学部応用生物科学科　動物資源開発学分野　和田研究室

ywada@cc.saga-u.ac.jp