佐賀大学農学部応用生物科学科 動物資源開発学分野 和田研究室
佐賀大学農学部応用生物科学科 情報基礎演習 講義テキスト 科目ホームページ
平均値の差の検定(t検定)
科学的な研究における研究計画と統計処理
科学的な研究を始める前には研究計画を立案します。
科学的な研究計画は以下のような手順で作成していきます。
- 問題意識の確認 何を明らかにしたいのか?
- 既知の研究成果の確認
- 研究に使えるリソースの確認
- 統計処理手法の確認
- 実験(調査)計画の立案
科学の世界において、実験や調査などの結果について議論するときに、統計学的検定を多用します。
統計的に有意かどうか(統計学的に意味がある差があるのかどうか)は非常に重要なことです。
より効率的な実験計画を立案するには、統計学的検定によって研究目的に沿った議論が可能かどうかを事前に検討しておく必要があります。
そのとき、通常は、研究における「作業仮説」を立てて、それを検証するような流れにします。
作業仮説とは、たとえば、「A遺伝子はBウイルスに対する免疫制御に関連している」というようなものです。
この作業仮説を立証するための実験計画を立てて、得られた結果を統計学的検定によって解析することになります。
具体的には、たとえば、Bウイルスを感染させた培養細胞(シャーレ3個)と感染させなかった培養細胞(シャーレ3個)からtotal RNAを抽出して、リアルタイムPCRを用いてA遺伝子の発現量を推定します。
そして、感染細胞と非感染細胞とでA遺伝子の発現量を統計学的に比較して、発現量に差があれば、「A遺伝子はBウイルスに対する免疫制御に関連している」と結論づけるわけです。
統計学的検定の流れ
最近はExcelの分析ツールを含めて統計処理が簡単にできるソフトが多く出回っています。
それを利用すれば簡単なのですが、中身を理解しておかないと、大変な誤解をする可能性もあります。
特に実験計画にマッチしていない統計手法を用いて得られた検定結果は、統計学的に意味がありませんので、注意してください。
統計手法が決まったら、まず、統計学的検定では、帰無仮説を設定します。
帰無仮説とは、上の例では、「発現量に差がない」というものです。
次に、それぞれの検定手法で必要な統計量を算出します。
その統計量と数表を比較して、この帰無仮説のもとで今回のデータが得られる確率(p値)を算出します。
これが小さければ小さいほど、帰無仮説の信頼性に疑問符が付くことになります。
通常、p<0.05 のとき、帰無仮説を棄却します(5%水準)。
すなわち、「発現量に有意差がある」と考えるわけです。
p<0.01のときは、高度に有意という言い方をします。
平均値の差の検定(t検定)とは
2集団間に差があるかないかを統計的に調べる方法を平均値の差の検定と言います。
統計学的にはt分布を使うのでt検定とも呼びます。
t検定には対応のあるデータに対するものと対応のないデータに対するものがあり、それぞれは若干計算方法が異なります。
対応のあるデータとは同じ個体群に対して時期をずらして2つの処理を行い、その処理間に差があるかないかを調べる場合などのことです。
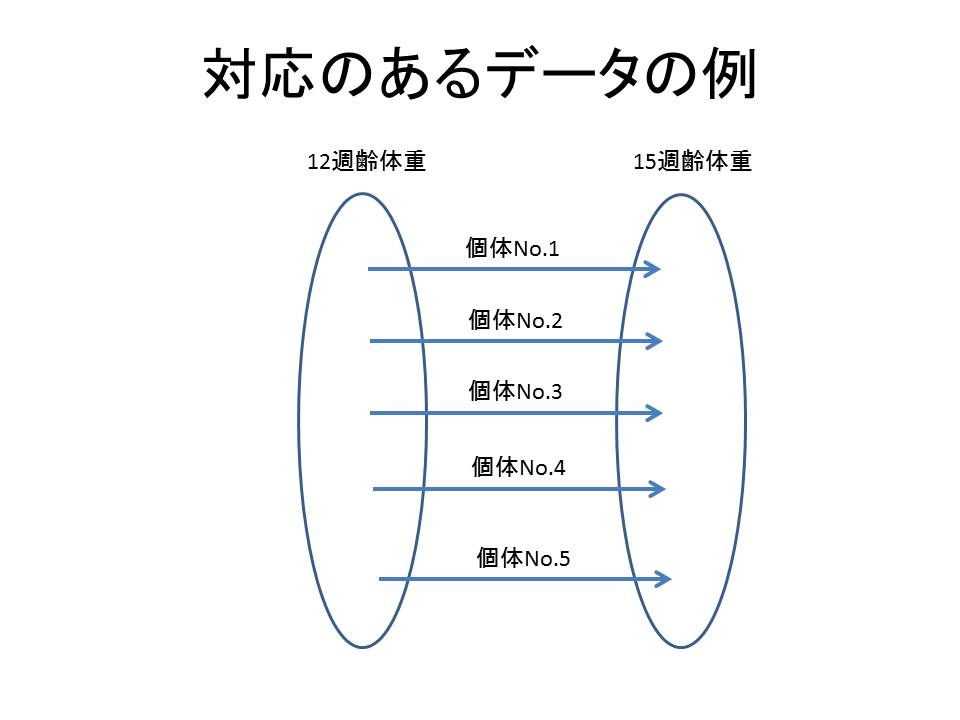
一方、対応のないデータとは、例えばウズラのLL系統とSS系統において産卵率に差があるかどうかを調べる場合などのことを言います。
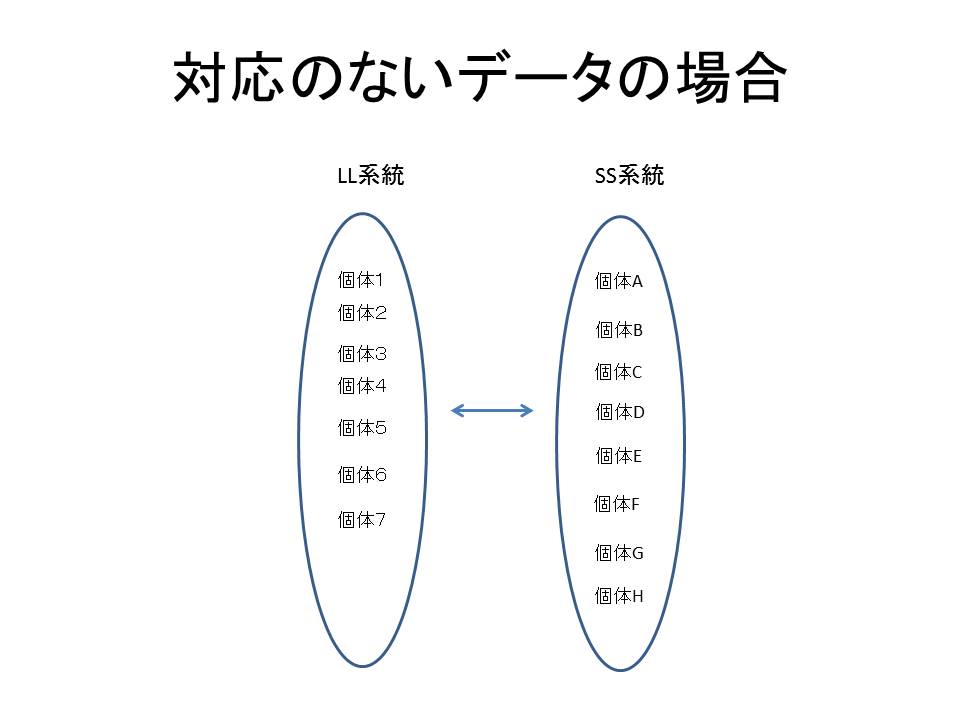
t検定における帰無仮説は「2集団の平均値に差がない」というものです。
計算したt値が当該自由度におけるt分布表の値よりも大きい場合、この帰無仮説は棄却されます。
すなわち、2集団間の平均値には有意差があるということになります。
詳しい理論と計算方法については数理統計学あるいは生物統計学の教科書などを参考にしてください。
この演習ではMS-Excelの分析ツールを用いた計算方法を示します。
対応のあるデータに対する平均値の差の検定
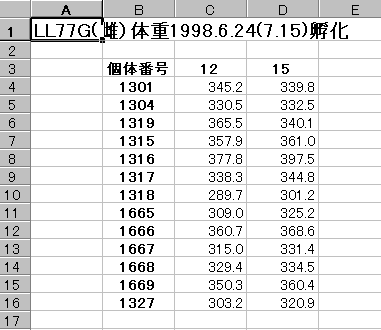
まず、MS-Excelを起動して、データを入力します。
ここでは、ウズラLL系統の同一個体群について、12週齢体重と15週齢体重に差があるかどうかを検定します。
「データ」の「データ分析」の「t検定:一対の標本による平均の検定」を選択します。「分析ツール」が見当たらない場合には、「アドイン」の「分析ツール」のところにチェックを入れてOKボタンを押してください。
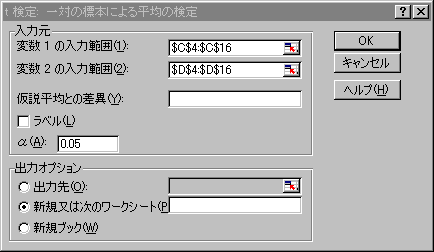
変数1の範囲に12週齢体重の範囲を、変数2の範囲に15週齢体重の範囲を指定して、OKボタンをクリックします。
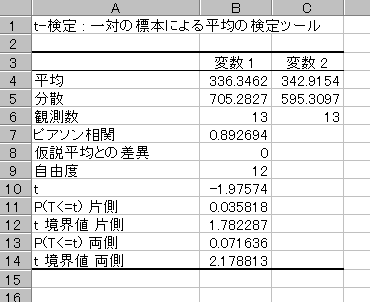
普通は自由度とt値についてt分布表を引いて検定するのですが、分析ツールではt分布表を引いた結果がすでに P(T<=t)両側 として示されています。
これは、帰無仮説が正しいにもかかわらず誤って帰無仮説が棄却される確率を表しています。
通常はP<0.05で5%水準で有意差ありと考えますので、LLの12週齢体重と15週齢体重には有意差がないという結論になります。
対応のないデータに対する平均値の差の検定
次に対応のない場合のt検定をやってみます。データとしてはウズラのLL系統とRR系統の8週齢体重を取り上げました。

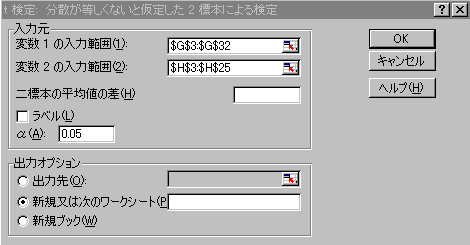
「データ」の「データ分析」の「t検定:分散が等しくないと仮定した2標本による検定」を起動します。
変数1の範囲にLLのデータの範囲を、変数2の範囲にRRのデータの範囲を指定してOKボタンをクリックします。
検定結果の見方は先ほどの場合と同じです。
P(T<=t)両側の値が1.16E-30となっていますが、これは 1.16に10のマイナス30乗をかけた値ということで、非常に小さな値です。
0.01よりも小さいですから通常は1%水準で有意差ありと判断します。
2集団間の等分散の検定(F検定)
上の例では2集団の分散が等しくないと仮定しました。
念のために、2集団間の等分散の検定をしておきます。
この検定はF分布を用いるのでF検定と呼ばれます。
「データ」の「データ分析」の「F検定:2標本を使った分散の検定」を起動して、先ほどと同じデータを変数1と変数2に指定してOKボタンをクリックします。
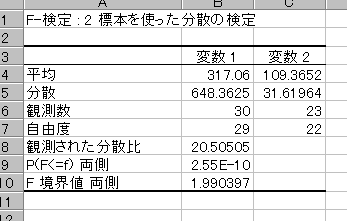
予想通り P(T<=t)両側の値は非常に小さいですね。
1%水準で2集団の分散には差があると言えます。
従って、先ほどのt検定で「分散が等しくない」と仮定したのは正しかったことが証明されました。

大学院生、編入学生、転学生、募集中!
最終更新年月日 2013年6月20日
佐賀大学農学部応用生物科学科 動物資源開発学分野
ywada@cc.saga-u.ac.jp









