佐賀大学農学部応用生物科学科 生物情報処理演習 講義テキスト 科目ホームページ
実験データを統計処理することはよく行われるが、その前に統計グラフを作成してデータの性質を良く吟味する必要がある。 グラフを見ることによって、直観的にデータの傾向を判断できることが多い。
もちろん、その後で正確な統計処理をして統計学的な判断を下さなければならないが、 統計グラフを作成することによって誤った統計手法の使用を防ぐことができる。
また、さまざまなオプションによって、細かな設定ができますが、あまりにも機能が多すぎて、初心者にはわかりにくくなってしまいました。
まず、Excelを起動してデータを入力します。

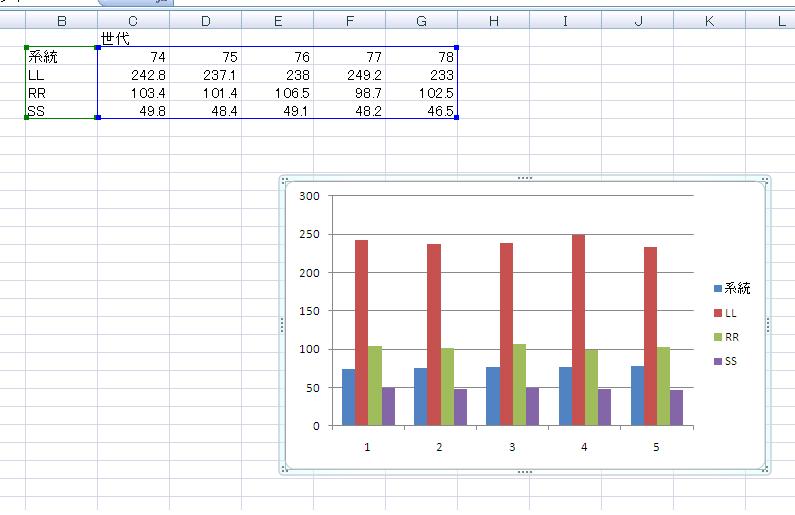
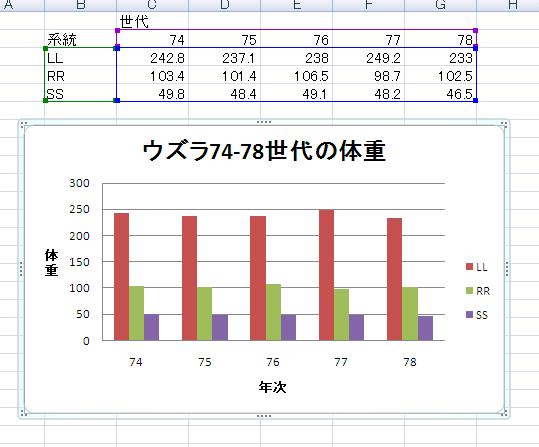
最初にデータ領域を選択し、「挿入」タブをクリックして、縦棒グラフをクリックし、左端のグラフを選択します。
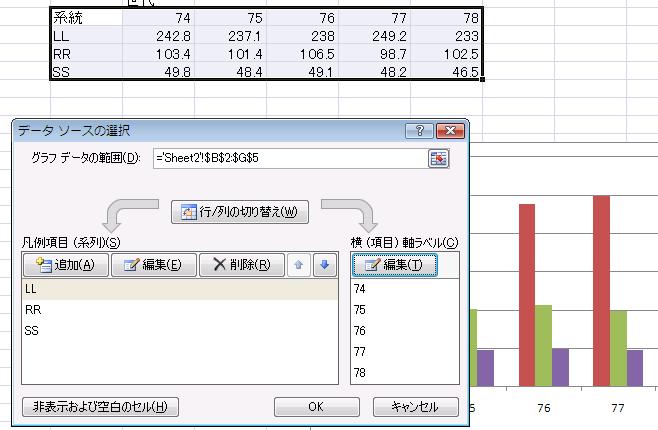
年次もデータになっているので、グラフの上で右クリックしてメニューから「データの選択」をクリックします。 左から系統を選択して削除し、横(項目)軸ラベルの編集をクリックして、年次のところをドラッグで指定します。
上部でグラフのレイアウトを指定し、タイトルを書きかえます。 上部の「レイアウト」をクリックして、軸ラベルから、主横軸ラベルと主縦軸ラベルを表示させるようにします。
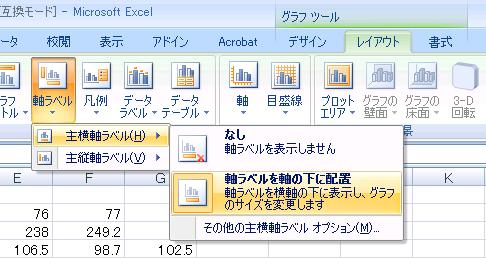
最後に軸ラベルを書きかえます。
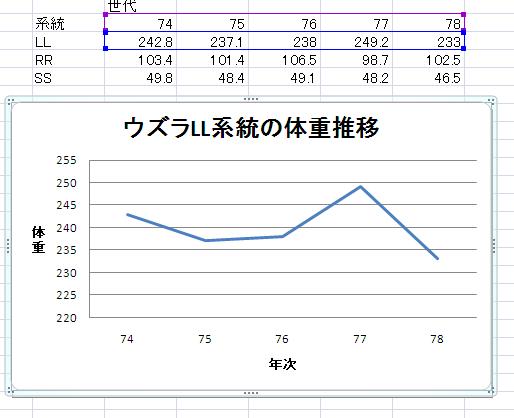
LL系統のデータについて折れ線グラフを書いてみました。 ここでは、「レイアウト」の凡例から「凡例なし」を選択しています。
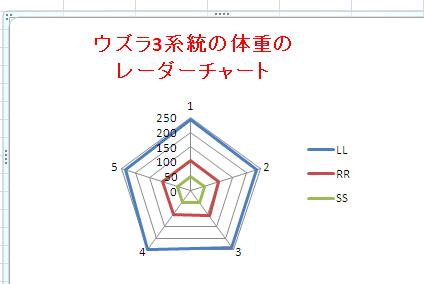
3系統のデータでレーダーチャートを書いてみました。 レーダーチャートはバランスを見るのにすぐれたグラフです。
具体的には(個々のデータ?平均値)/標準偏差を計算します。
Excelでは各系統の平均値は =AVERAGE(D3:H3)というように指定します。 最初に=があれば、Excelは式と認識します。
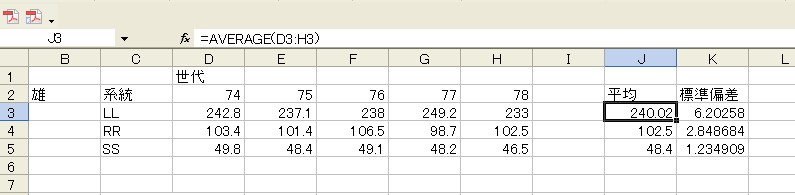
標準偏差STDEVも計算して、個々のデータと平均値、標準偏差から標準化したデータ表を作成しましょう。 D11に標準化した値を計算する式を入力します。 元のデータD3からLL系統の平均値を引いて、標準偏差で割っています。 そして、このセルの式を他のセルにもコピーすると簡単に標準化したデータ表が作成できます。
ただし、コピーのときにExcelは参照するセルの場所も移動させます。 個々のデータはそれでいいのですが、平均と標準偏差は1つの行では同じ値を参照しなければなりません。 そこで、動いてはいけないJ列とK列を指定する時に、$J3や$K3というように$をつけます。 これを絶対セルアドレスといいます。
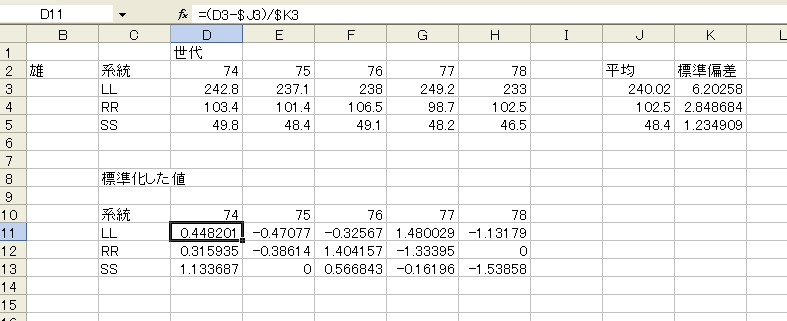
そして標準化したデータを折れ線グラフにすると同じレンジで各系統の6週齢体重の変化を見ることができます。
膨大なデータを入力するのは大変なので、今回は関数 f(x,y)=ax2+bxy+cy2 の データをExcelで計算して、そのデータに基づいた等高線グラフを作ってみましょう。
まず、a=-2, b=1, c=-3 で関数値を作成しましょう。 X座標、Y座標ともに-10から+10までの範囲で、1きざみで関数値を作ります。 そのために縦横に-10から+10まで1きざみでセルに値を入れていきます。
次にx=-10、y=-10となるC10のセルに関数式を入力します。 Excelではかけ算は*で、階乗は^で示します。
また、関数式をコピーする時に相対セルアドレスだと位置がずれてしまうので、 a,b,cの値の位置は$E$4のように絶対セルアドレスにしてください。 また、X座標の値は「9行」は固定ですので C$9 に、 Y座標の値は「B列」固定ですので、 $B10 と指定します。
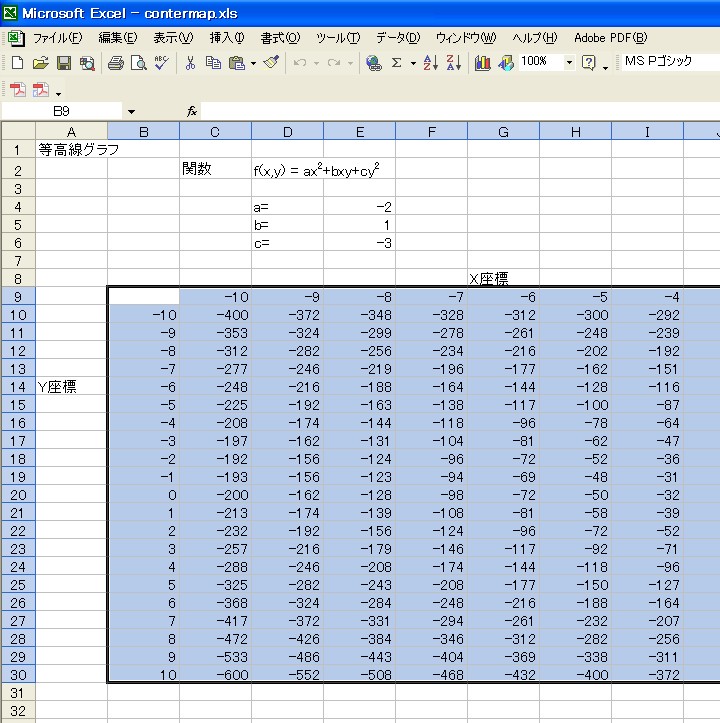
C10のセルへの入力が完了したら、関数範囲全体にC10の関数式をコピーしてください。
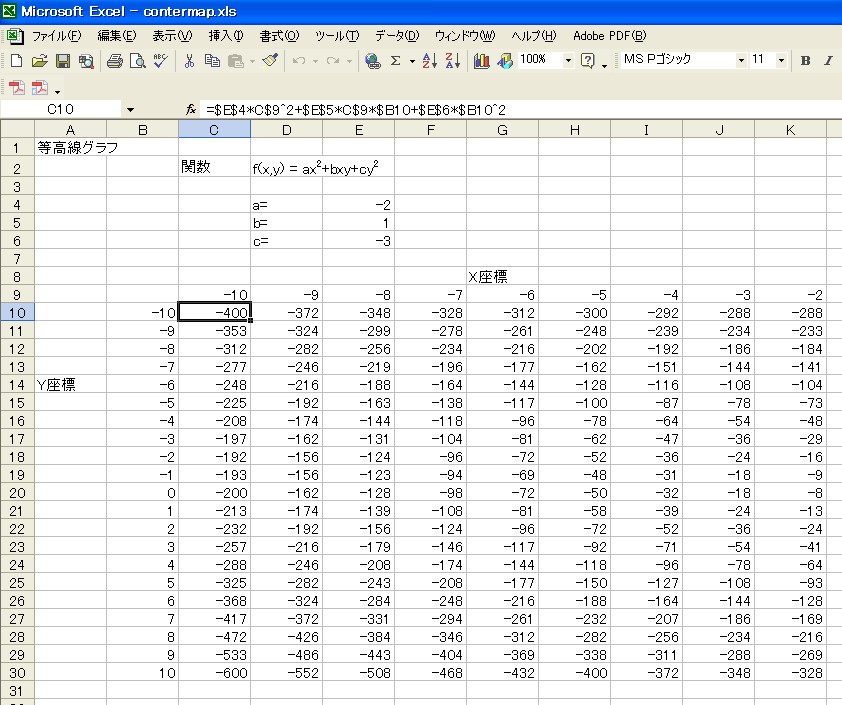
次にX座標、Y座標、関数値をすべて選択し、グラフウイザードの等高線を起動してください。
グラフタイトルなどを入力すれば等高線図のできあがりです。


最終更新年月日 2010年4月20日